In this second post of our Vision Transformer series, we describe how we applied model compression techniques, namely quantization and sparsity, to different versions of the Vision Transformer (ViT) and Data-efficient Image Transformer (DeiT) trained on the RESISC45 dataset. Compressing models enables more power efficient deployments on FPGA, by reducing the computation required in the algorithm. This is a key technique for enabling deployments on power sensitive systems such as a satellite, enabling a smaller FPGA to be used.
In this post, we show how the model accuracy is affected by different combinations of quantization and sparsity targets.
Model Compression through Quantization
The quantization process includes one or both of:
- Reducing the number of bits of the data type, e.g. use 8 bits instead of 32 bits.
- Using a less expensive format, e.g. use integer instead of floating point.
In this post we focus on post-training quantization, where numbers are quantized after training the model. Quantization is also possible during training, but we found we got good results with the post-training flow.
For the LEO project we have chosen 3 different quantization formats: TensorFloat32 (TF32), signed 8-bit integer (INT8) and half-precision floating point (FP16.16). They have been chosen as they are common amongst deep learning frameworks as well as CPUs and neural network accelerators.
The following image shows the number of bits allocated for the exponent E, mantissa M and sign S for the chosen numerical formats compared to single-precision floating point (FP32).
Quantization formats (Credits: image modified from “Achieving Low-latency Speech Synthesis at Scale” by Sam Davis)
Quantization can be exploited by a range of hardware platforms, making it a common technique for reducing the computation and power consumption required for a particular model.
Model Compression through Sparsity
Compression through sparsity works well when models are overparameterized, i.e. they contain more parameters than the ones needed to solve a specific task. This means that we can prune a significant number of weights (by setting their values to zero) without significantly affecting the accuracy of the model. In order to realise benefits through sparsity, hardware support is usually required, making different sparsity configurations more or less effective on different platforms.
There are many patterns that can be adopted to prune a model. On the one hand, there are structured sparsity methods where, for instance, in a 2D matrix, blocks of size n×m are enforced to be either all-dense or all-sparse. On the other hand there are unstructured sparsity methods that do not have any constraints on the sparsity pattern to follow. This typically results in the smallest quality degradation but it is also the most challenging sparsity pattern to deploy efficiently. Finally, there are methods that try to find a compromise between structured and unstructured patterns, since they share some characteristics with both of them. An example is the block balanced sparsity pattern that we have used for this project. We are going to refer to this as “2:4 sparsity” and it is the pattern supported by NVIDIA Ampere architectures. With this approach, each weight matrix is divided into blocks of 4 values and two values are pruned in each block.
An important question that has not been addressed yet is how to decide which weights to prune. The approach that we have followed is to prune the parameters that are closest to zero, a method known as magnitude-based pruning.
Magnitude-based pruning can be broadly classified as either one-shot, in which a trained network is pruned to the desired sparsity in a single step, or iterative, where the level of sparsity increases more gradually over the training process. In our experiments we have applied the one-shot method with the 2:4 sparsity pattern, as suggested by NVIDIA’s automatic sparsity library, and an iterative approach together with unstructured sparsity, following the cubic pruning schedule found in TensorFlow [1] as we find this approach works better for higher sparsity levels.
Sparsity patterns
Compressed Vision Transformer Experiments
We have conducted a large number of experiments using quantization, sparsity and combinations of both techniques. Since the number of experiments was very large, we are going to show only some of the results in this post. For the experiments that used distillation, we first trained a ResNet50 until convergence and then used it as a teacher for the DeiT student models. The accuracy of the teacher was 93.05%.
The experiments involved 3 different versions of the ViT and DeiT models, named Tiny, Small and Base. As mentioned before, the main difference between ViT and DeiT is in the training process (DeiT uses distillation). The approximate number of parameters for the three model version is:
- ~5.5 million for the Tiny version
- ~21.7 million for the Small version
- ~85.8 million for the Base version
The plots below show the results of the experiments done by applying only post-training Quantization. Dot-product operations in the attention layers are left unquantized. The results show that reducing the precision of the weights and the operations does not significantly affect the model accuracy, even when using just 8 bits and integer arithmetic (INT8). In addition to this, we can infer that in general DeiT models perform better than the correspondent ViT models, which means that training using both strong supervision and distillation from a CNN as a teacher provides a small improvement in the final accuracy using our dataset. This technique can enable up to a 4 times reduction in the size of the model weights when stored in memory, and inference performance speedups that depend on the platform being targeted.
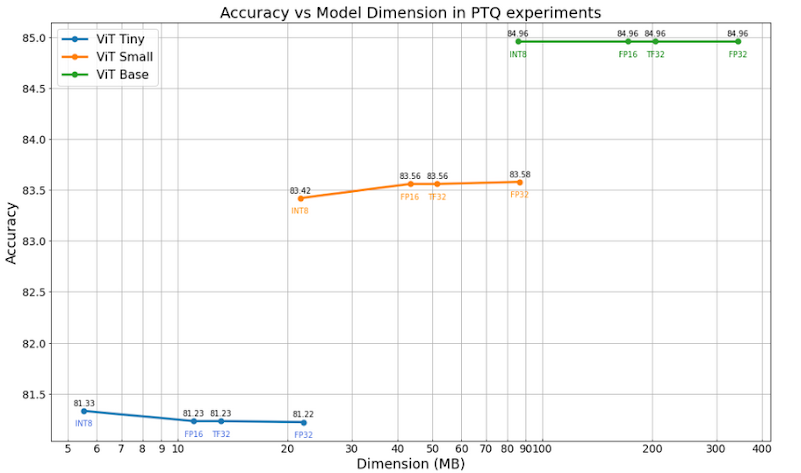
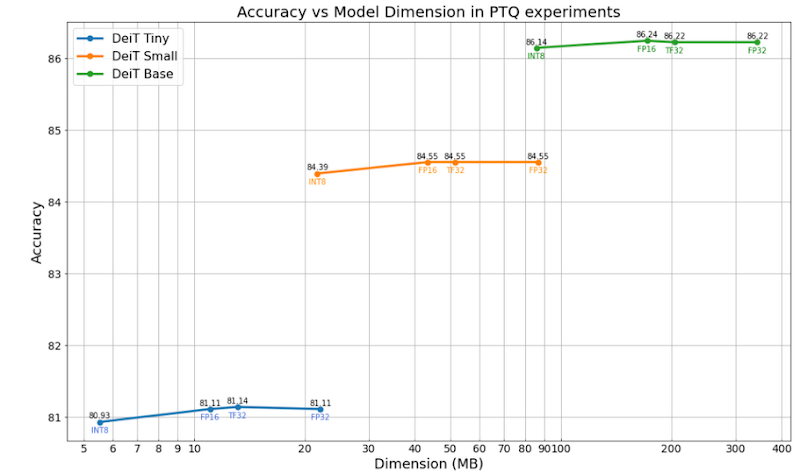
Accuracy of ViT/DeiT with different quantization schemes
Considering sparsity at FP32, the plots below show the results of our experiments. The numbers from 50% to 96.875% represent the sparsity targets that were used for the unstructured sparsity pattern, while “2:4” represents the NVIDIA 2:4 balanced sparsity described previously. The accuracy drops as the sparsity level increases. This is most evident with the Tiny models since the number of parameters of their dense counterpart is already quite low compared to the Small and Base versions. We can see that sparse versions of the Base model give better accuracy than an equivalent Small or Tiny model with an equivalent number of non zero weights. Low sparsity targets (50% and 75%) for the Small and Base versions of both the ViT and DeiT models actually perform even better than their dense counterparts, proving that these models were overparameterized and contain more parameters than needed for our dataset.
When sparsity is applied, the distillation used in the DeiT model still provides an additional boost in terms of accuracy compared to the respective ViT ones.
Using sparsity can enable performance improvements provided the platform used has the necessary support and we will consider this in our next post.
Accuracy of ViT/DeiT with different sparsity targets
When we combine quantization and sparsity, we find these results still hold true. The following plots show the model accuracy after applying a combination of both quantization and sparsity. The plot below demonstrates that the Base versions at high sparsity and low precision targets perform better than the Small and Tiny versions at lower sparsity levels with higher precisions, even though their dimension is almost the same. Another thing we can understand is that the unstructured sparsity pattern with 50% pruned parameters provides a better accuracy compared to the 2:4 block sparsity, even though they both eliminate 50% of the total model parameters. This results from the 2:4 block sparsity being more restrictive than unstructured sparsity in the way weights are pruned.
Accuracy of ViT/DeiT with different combinations of architecture size, quantization scheme and sparsity target
References
[1] H. Zhu, M.; Gupta, S. To prune, or not to prune: exploring the efficacy of pruning for model compression. https://arxiv.org/pdf/1710.01878.pdf

